Problem Statement:
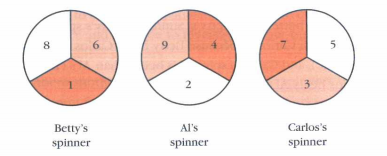
| We were presented with the following situation: there is a game of spinners where all three players spin their spinners and the one who lands on the highest number wins. The first part was to compare the spinners and see who's spinner was most likely to win. The second part of this problem was to try and create a new set of spinners to see if you could recreate the same pattern as the original set of spinners. |
My Process:
For this problem, I used skills that Ms. Chen taught me in sophomore year. I made a probability tree to compare the chances of one person winning over the other. After I got my results, I looked for patterns in the wheels to try and figure out why the answer was so interesting.
My SolutionFor part one, I found that there was no one person who had a better spinner. I learned this is called a non-transitive relationship. To re-create a set of spinners that could also have non-transitive relationships, I took a close look at the different sections of the spinners. I split them up and compared them based on their location, as you can see in the picture to the right. | |
Although I was unable to recreate a different set of spinners, I did find a pattern. Each section on the different spinners had a set of consecutive numbers. Each spinner had one section with the highest number, one section with the middle number and one section with the lowest number.
Problem Assessment
I thought the answer was really interesting because you would assume that in situations like these, a<b<c, but the answer was something more like a<b, b<c, and c<a. This relationship is called non-transitive, compared to the more straightforward transitive relationship (a<b<c). I thought this was a really interesting question and I think this would be a good challenge math problem. I will definitely remember non-transitivity because it came as a surprise to me. I also am not really sure how to recreate the spinner. I noticed a pattern but as hard as I tried, I couldn't make a different set of spinners.
Self Evaluation
With this problem, I grew a lot in my hypothesizing and experimenting abilities. I spent a lot of time trying to create a new and unique set of spinners that also had a non-transitive relationship. Although I was unsuccessful, I still think that persevering helped me develop my experimenting skills. I was looking for patterns in the spinners, but I couldn't replicate the pattern that I thought I was seeing. If there had been another pair of spinners, I think I could've maybe created another spinner. It's difficult to see patterns when you only have one example.
Even though I didn't find a different set of spinners, (starting to think there aren't any) I think that I still learned from this exercise. I got to explore transitive relationships and probability. I will definitely think about this in the future when it comes to probability and determining my odds or what the probability is of things coming out in my favor. Next time that I'm calculating my chances, I will remember that there is not always going to be one superior option.
Even though I didn't find a different set of spinners, (starting to think there aren't any) I think that I still learned from this exercise. I got to explore transitive relationships and probability. I will definitely think about this in the future when it comes to probability and determining my odds or what the probability is of things coming out in my favor. Next time that I'm calculating my chances, I will remember that there is not always going to be one superior option.
 RSS Feed
RSS Feed
