Problem Statement
Process
| We started by trying random numbers like 28 but then realized we should go in an order to see if we could find a pattern. we started with 01 and went in increasing order. We would write out what the numbers would be for each milepost and then figure out the miles traveled between each milepost. We knew the mileage had to be the same between the first and second milepost as the mileage between the second and third milepost. We started realizing that the mileage between each milepost was always a multiple of 9 but didn’t understand how that tied in. When finding the algebraic expression, we remembered that each distance traveled was a multiple of 9 and tried to include the number 9 in my algebraic terms. We saw that 16 was pretty close to 18, a multiple of nine so we set up 16 as (9*2)-2 and tried something similar for the next to mileposts. We realized they were both 2 miles short of a multiple of nine and went on to expand 61 to (9*5)-2 and 106 to (9*12)-2. Then we saw the pattern that each time you are multiplying 9 by 5 more than the last. |
Solution
9(2+(5(P-1)))-2=M. “P” being the post number, and “M” being the miles on the post.
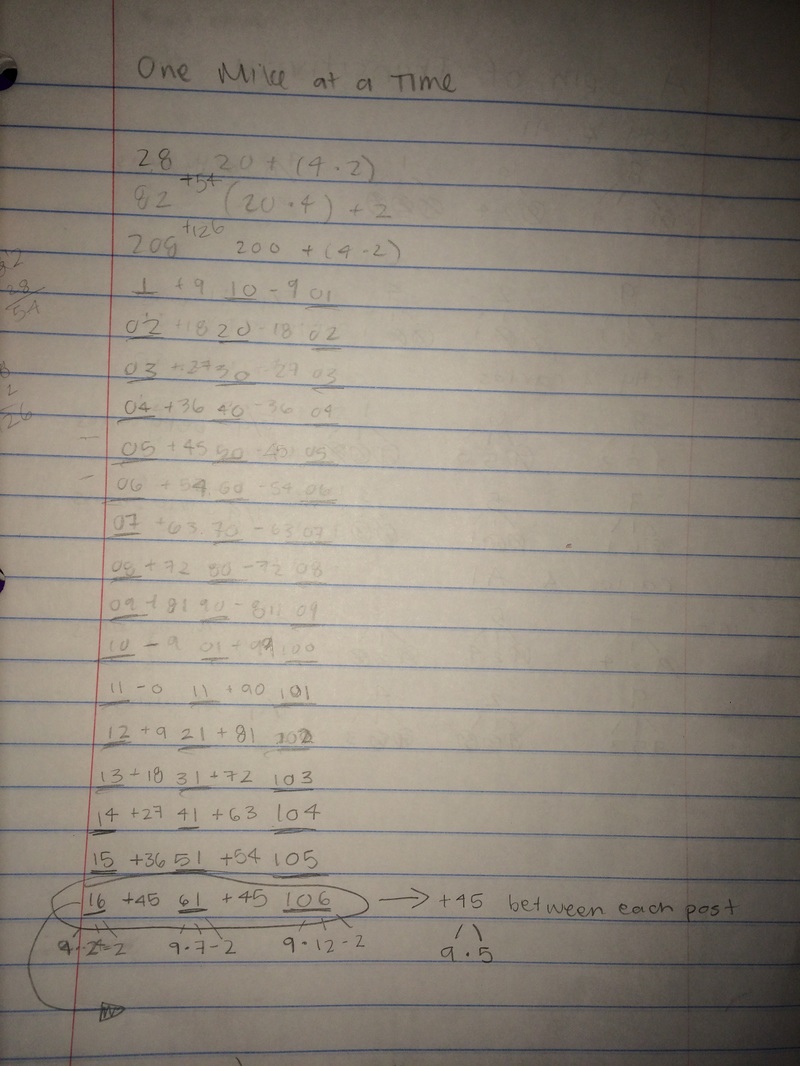
 RSS Feed
RSS Feed
